El Cuaderno Escocés

Ulam, Banach, Sierpiński, Mazurkiewicz, Janiszewski, Zaremba, Zygmund, Alfred  Tarsky, Kuratowsky … son nombres que destacan en la historia de la matemática moderna. Y todos ellos, sorprendentemente, coincidieron en un mismo lugar y en una misma época: Polonia, entre la primera y la segunda guerra mundiales, en la ciudad de Lvov, centro administrativo de la provincia de Lviv y también centro histórico de Galitzia, una región situada a caballo entre Polonia y Ucrania.

Lvov (en ruso), Lwów (en polaco) o Lemberg (en alemán), acreditan con sus diferentes nombres un pasado político agitado. Lugar de paso de las rutas comerciales que atravesaban los Cárpatos, la ciudad de Lvov recibió influencias culturales de ucranianos, polacos,  judíos,  austriacos,  armenios, húngaros, griegos, italianos, serbios y moldavos. Influencias que dejaron su impronta en las fachadas de las casas, en el sinuoso trazado de las calles, en la densa atmósfera de los bares y en el carácter alegre de sus habitantes.

En ese ámbito, mayoritariamente bohemio, en el que las ciencias podían ser arte y las artes ciencia, fue donde nació una de las más singulares creaciones de las matemáticas del siglo XX. Unas matemáticas que cimentaron sus conocimientos en el departamento de matemáticas de la Universidad de Lvov, pero que cobraron vida a tan sólo cien metros de allí, en el tumultuoso ambiente del Café Escocés.

Entre las cinco y las siete de la tarde, especialmente los sábados, cuando ya habían finalizado los seminarios en la Universidad de Lvov, el Café Escocés se convertía en lugar de peregrinación. A él concurrían químicos, físicos, pero sobre todo acudían matemáticos. Un grupo compacto, que formaba una tertulia cerrada y que podía ser fácilmente identificado como una «tribu» aparte. Algunos discutían problemas entre ellos, mientras otros, como Stefan Banach, miraban simplemente por la ventana o se acercaban al tablero de ajedrez, sobre el que sabían que Auerbach volvería a ganar inexorablemente de nuevo su partida.

En sus memorias Ulam escribió: «Me acuerdo de una sesión en el Café Escocés con Mazur y Banach que duró 17 horas sólo interrumpidas por las comidas. Lo que más me impresionaba era cómo se podía hablar de matemáticas, razonar y hallar demostraciones en esos debates». Esa maratoniana reunión dio como fruto un importantísimo teorema de análisis funcional. Cuando el café cerró, todos se marcharon cansados y satisfechos por los resultados obtenidos. Pero al día siguiente, que es cuando peligran los pequeños detalles de una demostración improvisada, se encontraron con que la mesa de mármol en la que habían estado trabajando resplandecía con un blanco luminoso. No quedaba ni rastro del teorema. Los matemáticos, encabezados por Banach, pusieron el grito en el cielo y el dueño del local les recordó, por si se les había olvidado, que el Escocés era un café y que una de las obligaciones del personal consistía en limpiar las mesas cada día antes de cerrar.

Fue entonces cuando intervino Lucja, la esposa de Banach, que le entregó a su marido un cuaderno que había elegido cuidadosamente, con las páginas en blanco y encuadernado con sólidas tapas de pasta. Le sugirió que anotaran en él las cosas importantes y que al finalizar la jornada se lo dieran a alguien para que lo guardase. El dueño del café fue el encargado de responsabilizarse del cuaderno. Cuando alguien del grupo lo pedía, se lo entregaba y al finalizar la jornada volvía a depositarlo tras la barra, en un lugar seguro. Esta pequeña complicidad hizo que el dueño del Café Escocés se sintiese definitivamente integrado en aquel grupo de «chalados».

Se decidió que en el cuaderno se anotarían los enunciados de los problemas al inicio de las páginas impares dejando el resto y el reverso en blanco para escribir la solución. El 17 de julio de 1935, Banach escribió el primer problema.

Había nacido el famoso Cuaderno Escocés.

Los contertulios

Al principio, el núcleo duro de la tertulia lo formaban Banach, Steinhaus y Mazur. No se aceptaba a estudiantes, aunque se hicieron dos excepciones, una con Stanislaw Ulam y otra con Josef Schreier. Al primero de ellos se deben la mayoría de datos que se conocen acerca del Café Escocés, recogidos en su autobiografía. Con el tiempo se sumaron a las reuniones otros matemáticos como Kaczmarz, Auerbach, Schauder, Kuratowski o Nikodym. Pero sin duda, el alma del Café Escocés fue Banach, uno de los matemáticos más excéntricos de su época. Odiaba los exámenes hasta tal punto que jamás se presentó a ninguno. Fue «descubierto» por Hugo Steinhaus, quien paseando un día por un parque oyó casualmente una conversación entre dos amigos que hablaban sobre la «medida de Lebesgue», una teoría matemática muy reciente. Steinhaus se metió en la conversación y quedó sorprendido por los conocimientos y el talento de Banach, que por aquel entonces era pasante en una oficina de ingeniería y que compensaba su exiguo sueldo dando clases particulares de matemáticas. Steinhaus consiguió convencerle para que entrara a formar parte de los círculos universitarios. En este sentido, Steinhaus afirmaba que Banach había sido su mayor descubrimiento en matemáticas. Gracias al valor y la originalidad de sus trabajos, Banach consiguió, aunque de forma totalmente irregular, que se le concediera el título de doctor, llegando a ser uno de los matemáticos más importantes del siglo.

Originariamente las tertulias matemáticas del politécnico de Lvov se celebraban en el Café Roma los sábados por la noche, coincidiendo con el final del seminario semanal de matemáticas. Pero un día, Banach se enfadó con el dueño porque éste no le fiaba las consumiciones hasta fin de mes, que es cuando cobraba el sueldo de la universidad. Decidió entonces trasladar la tertulia a otro local que estaba situado justo enfrente, que era precisamente el Café Escocés. Y fue así como la historia de lo que podría haber sido el Cuaderno Romano se convirtió en la historia del Cuaderno Escocés.

Con el tiempo, la fama de las tertulias matemáticas del Café Escocés traspasó fronteras, a ellas acudieron matemáticos del renombre de Lebesgue, Von Neumann, Frechet o Sierpinski. La mayoría de ellos dejó, como testimonio de su paso, un problema en el Cuaderno Escocés.

Los premios

La mayoría de los problemas que aparecen en el Cuaderno Escocés tienen adjudicado un premio, que, a modo de recompensa, acostumbraba elegir el mismo  autor  del  problema. La gama de premios es variopinta: una taza de café, 100 gramos de caviar, una  botella  de  whisky, una copa de coñac, una cena o un ganso vivo, eran algunos de ellos. También abundaban las invitaciones a comidas, aunque algunas, como la del matemático inglés en Cambridge o la fondue de Wavre en Ginebra, encerraban una cierta picaresca, ya que no incluían los gastos de viaje y de todos era sabida la precariedad económica de los participantes. Algunas propuestas eran más sofisticadas, como la de Von Neumann, quien prometió al que resolviera su problema una botella de «medida mayor que cero», refiriéndose a la teoría matemática de la medida.

El problema 153, propuesto por Mazur, que hacía referencia a bases de Schauder en espacios de Banach separables, permaneció sin resolver hasta 1972, año en que el matemático sueco Per Enflo encontró un contraejemplo. Obviamente, por entonces las tertulias del Café Escocés ya habían dejado de existir, pero aun así, en 1973 se celebró en Varsovia una emotiva ceremonia en la cual se entregó a Enflo un ganso vivo.

En 1998, el matemático inglés William T. Gowers recibió un premio no estipulado en el Cuaderno Escocés. Gowers resolvió, mediante técnicas combinatorias, varios de los problemas propuestos en el Cuaderno. Por este y otros trabajos adicionales, recibió la medalla Fields, el mayor galardón que se podía ofrecer entonces a un matemático.

La guerra

En abril de 1939, Banach fue elegido presidente de la Academia de Matemáticas polaca y en junio de ese mismo año, dicha institución le otorgó un premio que, además de honores, suponía una importante cantidad de dinero en metálico, la primera de la que Banach podría gozar en su vida. Pero tres meses después, los soviéticos ocuparon Lvov y congelaron todas las cuentas bancarias, de manera que Banach nunca llegó a cobrar su premio. Y las cosas siguieron más o menos igual. Durante los dos años que duró la primera ocupación soviética, en el Cuaderno Escocés aparecen problemas propuestos por matemáticos rusos de la talla de Aleksandrov, Sobolev o Lusternik.

Para cuando los nazis ocuparon Lvov, ya se había tomado la decisión de poner a buen recaudo el famoso cuaderno de problemas. Lo guardaron en la caja de las piezas del ajedrez y luego la enterraron esta junto a uno de los postes de la portería de fútbol del estadio de la ciudad. Los nazis mataron a varios de los matemáticos del grupo (Schauder, Auerbach y Kaczmarz, entre otros). Ulam huyó a Estados Unidos, donde fue figura destacada del programa nuclear, y Banach consiguió sobrevivir a la conflagración, pero murió poco después de que los rusos ocuparan de nuevo Lvov.

Después de la guerra Steinhaus recuperó el cuaderno, lo copió a mano y en 1956 le envió una copia a Ulam. Éste lo tradujo al inglés y luego envió 300 copias a diferentes universidades de todo el mundo. A partir de entonces, el Cuaderno Escocés se convirtió en leyenda.

Antes de morir, Banach lo legó a su hijo Stephan, un neurocirujano que actualmente ejerce en Varsovia y que posee el único original que existe del Cuaderno Escocés.

La última anotación que contiene el Cuaderno está datada el 31 de mayo de 1941 y es de Steinhaus.

El problema número 19

Quizás uno de los problemas más populares del Cuaderno Escocés fue el número 19. Al menos, su enunciado es lo bastante inteligible para cualquiera que conozca los rudimentos de la geometría y el principio de Arquímedes. Fue propuesto por Ulam en los siguientes términos: «Si un sólido de densidad uniforme tiene la propiedad de flotar en equilibrio en cualquier posición en la que se le deje ¿deberá ser éste necesariamente una esfera? En particular, cuando la densidad es cero: si un sólido descansa en equilibrio en cualquier posición en la que se le deje sobre una superficie plana horizontal, ¿deberá ser éste una esfera?»

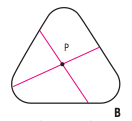
La segunda parte del problema, cuando la densidad es cero, tiene una respuesta afirmativa, pero el caso más general sigue siendo actualmente una cuestión abierta. Hay, sin embargo, una versión bidimensional del problema que encierra algunos aspectos curiosos. Para poder imaginar una versión en dos dimensiones, lo mejor es pensar que la figura en cuestión tiene forma cilíndrica. Un cilindro circular permanece flotando en equilibrio en cualquier posición que se le deje, siempre y cuando se restrinjan las posiciones a una sección transversal plana. En estas condiciones está claro que un círculo permanece en equilibrio sea cual fuere la posición en que lo dejemos. Pero un círculo es una figura que tiene, entre otras, una propiedad interesante. Posee un punto P, que coincide con el centro de la circunferencia, tal que cualquier segmento que pase por él divide, tanto al perímetro como al área del mismo, en dos partes que son iguales entre sí. Sin embargo, las circunferencias no son las únicas figuras que poseen esta propiedad. En 1921, el matemático austriaco K. Zindler (1866-1934) encontró la manera de construir  figuras,  conocidas con el nombre de «curvas de Zindler», que presentaban esta  propiedad.  Se construyen de forma ingeniosa a partir de curvas de anchura constante. Por ejemplo, la figura (B) posee un punto P tal que todo segmento que pase por él divide  el perímetro y el área en partes iguales.

Otra de las figuras de Zindler es el "Corazón", llamada así porque su forma es muy parecida a un corazón (C).

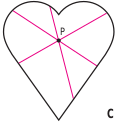
Y que también contiene un punto P con la propiedad de que todas las rectas que pasan por él dividen, tanto al perímetro como a la superficie en dos partes iguales.

El caso es que H. Auerbach, aquel al que nadie conseguía ganar al ajedrez en el Café Escocés, demostró en 1938 que cuando la densidad del líquido era 1/2, las figuras de Zindler quedaban flotando en equilibrio en cualquier posición en que se las dejara.