Cónicas y Cuádricas

Los sólidos platónicos obedecen más a representaciones mentales que a la percepción directa de objetos; en cambio, las cónicas y las cuádricas son las curvas y superficies más familiares de la geometría y las encontramos indefectiblemente en nuestro entorno más inmediato. Las cónicas aparecen en las órbitas de los planetas, en las lentes ópticas, en las trayectorias de cohetes y proyectiles. Podemos observar cuádricas en las antenas parabólicas, en estructuras arquitectónicas, en las chimeneas de centrales térmicas, en multitud de recipientes de la vida cotidiana, como copas, vasos o cuencos y hasta en las sillas de equitación. Llegar a determinar las ecuaciones analíticas de todas estas superficies, clasificarlas, calcular sus longitudes, superficies y volúmenes, ha sido una larga tarea de la que se han ocupado los matemáticos más ilustres y ramas de las matemáticas tan cruciales como la geometría, el álgebra o el cálculo diferencial.

Cónicas

Se designan como cónicas no degeneradas las curvas que se obtienen al cortar mediante un plano un cono de dos hojas. Cuando dicho plano es perpendicular al eje del cono se obtiene una circunferencia; si es paralelo a dicho eje, una hipérbola, y en los demás casos se obtiene una parábola. A la elipse y a la hipérbola se las conoce como cónicas con centro (la circunferencia es de hecho un caso particular de elipse). Las secciones cónicas ya eran conocidas por los griegos (existe un estudio detallado de las mismas en las obras de Apolonio). También fueron ampliamente estudiadas por J. Kepler para la determinación de las órbitas planetarias y por I. Newton, que fue quien estableció las leyes físicas a partir de las cuales puede demostrarse que dos masas sometidas únicamente a su atracción gravitatoria mutua orbitan una alrededor de la otra siguiendo trayectorias cónicas (problema de los dos cuerpos).

Definición y ecuaciones

Circunferencia: Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado centro. El radio de la circunferencia es la distancia al centro de un punto cualquiera de dicha circunferencia.

$$ \displaylines{Ecuación \ reducida \\ x^{2}+y^{2}=r^{2} \\ Ecuación \ general \\ x^{2}+y^{2}+Dx+Ey+F=0} $$

Elipse: Lugar geométrico de los puntos del plano cuya suma de distan-cias a dos puntos fijos es constante. Estos dos puntos fijos se llaman focos de la elipse.

$$ \displaylines{Ecuación\ reducida \\ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 \\ Ecuación\ general \\ Ax^{2}+Bx^{2}+Cx+Dy+E=0} $$

Hipérbola: Lugar geométrico de los puntos del plano cuya diferencia de distancias entre dos puntos fijos es constante. Estos dos puntos fijos sellaman focos de la hipérbola

$$ \displaylines{Ecuación\ reducida \\ \frac{x^{2}}{a^{2}}-\frac{y^{2}}{b^{2}}=1 \\ Ecuación\ general \\ Ax^{2}-Bx^{2}+Cx*Dy+E=0} $$

Parábola: Lugar geométrico de los puntos del plano que equidistan de un punto fijo llamado foco y de una recta fija llamada directriz.

$$ \displaylines{Ecuación\ reducida \\ x^{2}=4cy \\ Ecuación\ general \\ x^{2}+Dx+Ey+F=0} $$

Cuádricas

	Con centro	Elipsoide
		Hiperboloide	una hoja
			dos hojas
CUÁDRICAS	Sin centro	Paraboloide	Elíptico
			Hiperbólico
	Degeneradas	Cilindros
		Conos

Existen ciertas analogías entre las cónicas y las cuádricas que relacionan elipses con elipsoides, hipérbolas con hiperboloides y parábolas con paraboloides. La analogía, por supuesto, va más allá de una pura nomenclatura y se pone de manifiesto cuando se hacen cortes de una cuádrica mediante un plano y aparecen las secciones cónicas. Dicho de una forma un tanto imprecisa: las cuádricas están construidas a base de cónicas.

Elipsoides

Los elipsoides responden a una ecuación general del tipo

$$ \frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}} + \frac{z^{2}}{c^{2}}=1 $$

En general, las secciones hechas por planos perpendiculares a cualquiera de los tres ejes de coordenadas dan como resultado elipses de diferentes tamaños y formas, algo que se deduce directamente de la ecuación ya que si, por ejemplo, cortamos por un plano $z = k $ nos queda la ecuación:

$$ \frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}}=1 - \frac{k^{2}}{c^{2}} $$

que es la ecuación de una elipse de semiejes $a$ y $b$ con centro en el punto $(0, 0, k)$.

En el caso en que dos de los parámetros $a, b, c $sean iguales se tiene un tipo particular de elipsoide denominado esferoide, que es la forma que tienen las pelotas de rugby. Se puede obtener como una superficie de revolución lograda haciendo girar una elipse alrededor de su eje mayor. Y en el caso en que los tres parámetros sean iguales, lo que se obtiene es una esfera.

Hiperboloide de una hoja

Tiene por ecuación:

$$ \frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}} - \frac{z^{2}}{c^{2}}=1 $$

Se trata de una superficie reglada, puesto que contiene rectas.

Las secciones por planos perpendiculares al eje $z$ dan elipses (o bien circunferencias en el caso en que $a = b$) y las secciones por planos paralelos a dicho eje, ramas de hipérbola. El hiperboloide de una hoja también puede interpretarse como una superficie de revolución obtenida al hacer girar una hipérbola alrededor de la recta perpendicular por el punto medio a la recta que une los focos.

Hiperboloide de dos hojas

Es la superficie que define la ecuación:

$$\frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}} - \frac{z^{2}}{c^{2}}=-1$$

Se puede conseguir como superficie de revolución haciendo girar una hipérbola alrededor de la recta que une los focos.

Las secciones obtenidas por planos perpendiculares al eje $z$, es decir por planos de ecuación $z = k$ son elipses reales si $|k| >c$, e imaginarias en caso contrario.

Paraboloide elíptico

Viene dado por la ecuación:

$$\frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}}=2z$$

Las secciones por planos $x = k$, es decir, planos perpendiculares al eje $x$, nos dan parábolas y las secciones $z = k$, es decir por planos perpendiculares al eje z, nos dan elipses (siempre y cuando sea $k > 0$).

La mayoría de las antenas de recepción por satélite tienen esta forma (de ello deriva la expresión popular «colocar una parabólica en el terrado»).Los paraboloides elípticos son la forma que adoptan en general tanto las antenas de telecomunicación (antenas parabólicas para la recepción vía satélite) como las de los radiotelescopios de los observatorios astronómicos de todo el mundo que captan las ondasde radio procedentes del espacio.

Paraboloide hiperbólico

Esta tal vez sea la más complicada de todas las cuádricas, pero también la más fácil de imaginar si pensamos en una silla de montar.Tiene por ecuación cartesiana:

$$\frac{x2}{a^{2}} - \frac{y^{2}}{b^{2}}=2z$$

Un plano perpendicular al paraboloide hiperbólico que no pase por su centro corta a éste en una hipérbola, cuyas ramas se encontrarán dispuestas en el plano $XY$ en un lado o en el opuesto, según que el mencionado plano corte por encima o por debajo del origen de coordenadas. Al cortarla por un plano que pase por el origen de coordenadas, lo que se obtienen son dos rectas que se intersecan en el citado origen (una cuádrica de generada).

En cambio, el corte por un plano que sea paralelo al eje $z$ da como resultado una parábola, que será más o menos cóncava según que el plano que interseca al paraboloide hiperbólico se encuentre más o menos alejado del origen de coordenadas.

Superficies regladas y de revolución

Superficies regladas son aquellas que pueden ser generadas por el movimiento de una recta que se designa con el nombre de generatriz de la superficie. Se trata por tanto de superficies que contienen rectas. En ocasiones no es fácil, a simple vista, decidir si una superficie es o no es reglada. Para averiguarlo hay que comprobar si sobre la superficie en cuestión se puede apoyar el canto de una regla, de ahí el nombre de reglada. El hiperboloide de una hoja y el paraboloide hiperbólico son ejemplos de superficies regladas.Algunas de estas superficies poseen la propiedad adicional de que tienen un único plano tangente a lo largo de cada generatriz, lo cual significa que tienen un desarrollo plano, es decir, que se pueden extender sobre una superficie plana, como es el caso de un cilindro, motivo por el que reciben también el nombre de superficies desarrollables. No todas las superficies regladas son desarrollables. Así, los dos ejemplos anteriores, el hiperboloide de una hoja y el paraboloide hiperbólico, son superficies regladas que no son desarrollables. Las superficies de revolución, por el contrario, son las que se obtienen al hacer girar una curva alrededor de un eje, aunque cabe recordar que, en este contexto, una recta se considera un caso especial de curva. Por lo tanto, son cuádricas de revolución, por ejemplo,el cilindro o el cono.

Conos

Un cono podría ser considerado en general como una pirámide cuyas secciones rectas son circunferencias. En el caso de que dichas secciones sean elipses se habla de un cono elíptico. Su ecuación cartesiana viene dada por

$$\frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}} - \frac{z^{2}}{c^{2}}=0$$

Cilindros

Si tomamos una recta perpendicular al plano definido por una cónica cualquiera, la superficie engendrada por dicha recta al recorrer la cónica es un cilindro. Se tiene por tanto un cilindro circular si dicha cónica es una circunferencia, y elíptico, parabólico o hiperbólico en el caso en que la cónica sea, respectivamente, una elipse, una parábola o una hipérbola.

Ecuaciones canónicas

La cónica que nos resulta más familiar es sin duda la circunferencia. Tiene una definición sencilla como lugar geométrico de los puntos del plano que equidistan de un punto llamada centro. Y también tiene una ecuación cartesiana simple: $x^{2}+y^{2}=R^{2}$ en donde $R$ es el radio de la circunferencia.

Vamos a ver una representación gráfica en un caso concreto en que $R = 3$.

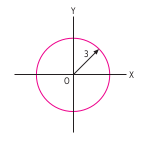
La ecuación anterior será entonces $x^{2}+y^{2}=9$. Es una ecuación sencilla porque la circunferencia tiene su centro en el origen de coordenadas. Si desplazamos dicho centro hasta el punto $(1, 2)$, la ecuación cambiará mucho de aspecto:

$$x^{2} + y^{2} - 2x - 4y - 4 = 0$$

Supongamos que hubiéramos partido de esta ecuación. En principio nos resultaría difícil identificarla como la ecuación de una circunferencia de radio $3$. Vamos a hacer un pequeño experimento que consiste en trasladar el origen de coordenadas desde el punto $(0, 0) $hasta el punto $(1, 2)$. Para ello hay que hacer un cambio de coordenadas que vendrá dado por las ecuaciones

$$ \displaylines{x'=x-1 \\ y'=y-2} $$

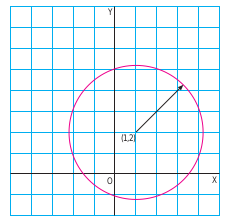
Sustituyamos ahora las nuevas coordenadas en la ecuación de la circunferencia:

$$(x+y)^{2} + (y+2)^{2} - 2(x+1) - 4(y+2) - 4=0$$

Haciendo operaciones queda $x^{2}+y^{2}=9$, que era la ecuación original. Esta última forma recibe el nombre de ecuación canónica o reducida de la circunferencia. No vamos ahora a entrar en detalles, pero existe un algoritmo relativamente sencillo para obtener de la ecuación general de una circunferencia su forma canónica que se enseña en loscursos elementales de matemáticas. Lo que queremos poner de manifiesto es un grado de dificultad que va en aumento cuando la cónica en cuestión se va haciendo más compleja. La circunferencia es una figura que presenta una simetría total con respecto al centro, por lo que para obtener la ecuación canónica únicamente debemos conseguir ubicar su centro en el origen de coordenadas. Pero este no es el caso, por ejemplo, de una elipse, que no presenta las mismas simetrías que una circunferencia, ya que tiene dos ejes diferentes y puede por tanto estar orientada en el plano de diversas formas.La ecuación canónica de una elipse de semiejes $a$ y $b$

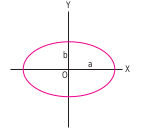
viene dada por

$$\frac{x2}{a^{2}} + \frac{y^{2}}{b^{2}}=1$$

lo cual significa que la elipse tiene su centro en el origen de coordenadas y que las direcciones de los semiejes se corresponden con la dirección de los ejes de coordenadas. Pero una elipse que no esté en esta posición tendrá una ecuación muy diferente, como por ejemplo $3x^{2}+2xy+3y^{2}+16x+16=0$. Reducir a la forma canónica una cónica cualquiera (a) supondrá, en el caso más general, tener que hacer dos movimientos: de traslación del origen de coordenadas al centro de la cónica (b) y después un giro de los ejes para dejarlos en la misma dirección que los ejes principales de la cónica (c).

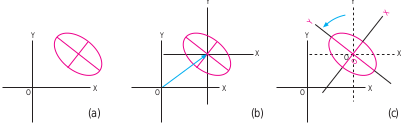
Lo que en principio no se presenta como una tarea fácil si no tenemos un algoritmo general que nos permita hacerlo. Una tarea que se puede complicar considerablemente cuando trasladamos el mismo problema del plano al espacio y lo que tratamos es de encontrar un método por el cual podamos dilucidar que una ecuación como $9x^{2}+2y^{2}-4z^{2}-12xy-12xz-2x+24y+14z-5=0$ representa a un paraboloide hiperbólico.

Un largo camino

Conseguir reducir las ecuaciones de las cónicas y las cuádricas a base de elegir unos ejes de coordenadas que tuvieran la orientación de los ejes principales se hacía a base de métodos de cálculo que ya eran conocidos en el siglo XVIII, pero la clasificación cuando la ecuación ya estaba reducida aparece por primera vez en la obra de Cauchy Lecciones sobre las aplicaciones del cálculo infinitesimal, una obra publicada en 1826. El sistema se basaba en el número de términos positivos y negativos que aparecían en la forma canónica y no se sabía con certeza si esa secuencia de signos permanecía invariable frente a los cambios de coordenadas. Sylvester estableció una ley para las formas cuadráticas de $n$ variables, pero no aportó ninguna demostración. Serían Jacobi y con posterioridad Gauss, quienes demostraron, mediante la introducción de la llamada ecuación característica, el teorema de invariancia para la reducción de formas cuadráticas. Ya a principios del siglo XX, con el desarrollo de la Geometría Analítica, el estudio de las funciones homogéneas encontró una metodología adecuada para su reducción a formas canónicas, especialmente con la introducción de coordenadas homogéneas. De esta forma se cimentaron los conceptos para que el estudio y la clasificación de cónicas y cuádricas pasara a ser un capítulo más dentro de una geometría mucho más general que fue la Geometría Proyectiva.

Kepler y el tonelero

Los grandes depósitos de combustible que pueden verse en las terminales de los aeropuertos suelen estar formados por un cilindro y dos paraboloides circulares en los extremos (también muchos depósitos de gas tienen esta forma). Una manera de saber el volumen de líquido que contienen es introducir verticalmente una varilla en la que se han hecho unas marcas que indican el volumen en función de la altura. Realizar esas marcas, que son específicas para la forma de cada depósito, es un problema que atañe a las cuádricas y al cálculo integral (concretamente es un problema que se resuelve por integrales dobles o triples). Kepler fue uno de los primeros matemáticos en plantearse este tipo de problemas y además lo hizo en unas circunstancias un tanto especiales, concretamente la fecha en que contrajo matrimonio en segundas nupcias (su primera esposa había fallecido dos años antes) con Susanne Reuttinger. Se trataba de un matrimonio de conveniencia, ya que Kepler necesitaba urgentemente de una mujer que cuidara de él y de sus hijos y se hiciese cargo de las tareas domésticas. Alguien debió de advertir a Susanne del peculiar carácter de su futuro marido, ya que no se sorprendió cuando éste abandonó la fiesta para estudiar detenidamente la operación que un bodeguero estaba realizando en los toneles que contenían el vino destinado a los comensales que concurrían a la fiesta. No sólo la forma de los recipientes no era cilíndrica por completo, sino que además la medición se hacía introduciendo una varilla oblicuamente a través de la tapa. El resultado de esta reflexión fue su obra Nova stereometria doliorum vinariorum («Nuevo método de medición de barriles de vino»), publicada en 1615. Pararesolver el problema, Kepler se basó en la técnica de los indivisibles que había desarrollado Arquímedes. Tiempo después, el método fue perfeccionado por Bonaventura Cavalieri (1598-1647). Se podría afirmar que en aquella boda se establecieron las bases de lo que habría de ser el futuro Cálculo Infinitesimal.